区间DP之多边形三角剖分的最低得分[Cuckoo]

区间DP模板
for (int len = 2; len <= n; len++) {//区间长度
for (int i = 1; i <= n; i++) { //枚举起点
int j = i + len - 1; //区间终点
if (j >= n) break; //防止越界
for (int k = i+1; k < j; k++) { //枚举分割点,开始转移
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + w[i][j]);
}
}
}
定义状态
dp[i][j]表示从凸多边形从A[i...j]这个范围内,进行剖分所能得到的最低分
转移方程
dp[i][j] =min{dp[i][k]+dp[k][j]+A[i]*A[k]*A[j]} k>=i+1 && k<=j-1
要求的是dp[0][n-1]即A[0...n-1]范围内的多边形剖分后的最小值
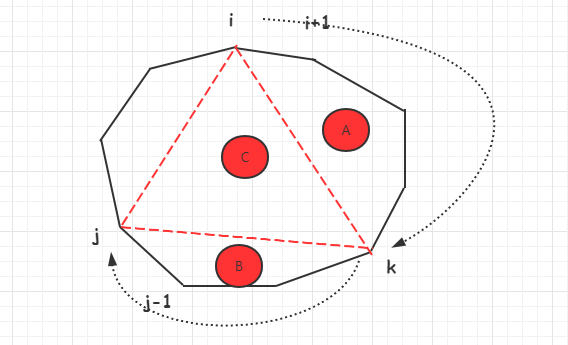
如上图: A部分是dp[i][k] B部分是dp[k][j] C部分是A[i]*A[k]*A[j]
public int minScoreTriangulation(int[] A) {
int INF = Integer.MAX_VALUE >> 1;
if (A == null || A.length == 0) return 0;
int n = A.length; //
int[][] dp = new int[n][n];
for (int len = 2; len <= n; len++) {
for (int i = 0; i < n; i++) {
int j = i + len; //当i=0,len=2时,即[0,2] 三角形必须要三个点才能形成
if (j >= n) break; //
dp[i][j] = INF; //要找最小值,默认是0,设置为INF
for (int k = i + 1; k < j; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[k] * A[j]);
}
}
// PrintUtils.printMatrix(dp);
}
return dp[0][n - 1]; //返回的是A[0...n-1]这个区域的剖分后的最小值
}
//打印的dp A:[1, 3, 1, 4, 1, 5]
0 0 3 7 8 13
0 0 0 12 7 22
0 0 0 0 4 9
0 0 0 0 0 20
0 0 0 0 0 0
0 0 0 0 0 0
另外一种写法
len从3开始,那j需要-1,即j=len+i-1
public int minScoreTriangulation(int[] A) {
int INF = Integer.MAX_VALUE >> 1;
if (A == null || A.length == 0) return 0;
int n = A.length; //
int[][] dp = new int[n][n];
for (int len = 3; len <= n; len++) {
for (int i = 0; i < n; i++) {
int j = len + i - 1;
if (j >= n) break;
dp[i][j] = INF;
for (int k = i + 1; k < j; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[k] * A[j]);
}
}
// PrintUtils.printMatrix(dp);
}
return dp[0][n - 1];
}
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/10/29/minimum-score-triangulation-of-polygon/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)