数组模拟邻接表
头插法
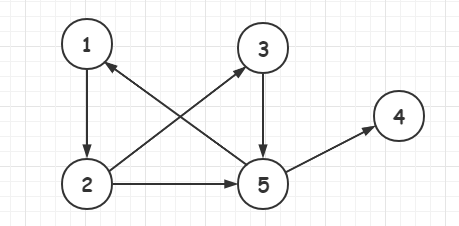
数组表示无权值有向图的邻接链表
int E = 6;// 边的总数量,当图为无向图时,一条边的两个端点建立邻接表时,均会记录该边,一条边会被记录两次
int V = 5; //顶点的总数量
int idx = 0; //标记当前边的编号
int[] head = new int[V + 1]; //每个顶点其中一条边的编号 下标从1开始的 +1
Edge[] edge = new Edge[E + 1]; //边的数量 下标从1开始的 +1
class Edge {
int to; // 边所指向的点
int next; //下一条边的编号
public Edge() {
}
public Edge(int to, int next) {
this.to = to;
this.next = next;
}
}
//u是起点,v是一条边的终点,添加一条边
private void addEdge(int u, int v) {
edge[++idx].to = v; //当前边的指向v
edge[idx].next = head[u]; //在u顶点的邻接表这个栈的顶部加入一条边(头插法)
head[u] = idx;//top为加入边的编号,加入后要更新head,使得head记录邻接表栈顶边的编号
}
private void print() {
for (int i = 1; i <= V; i++) {//遍历所有顶点
System.out.printf("%d\n", i);
for (int j = head[i]; j != -1; j = edge[j].next) {
System.out.printf("--> %d\n", edge[j].to);
}
}
}
//初始化
private void init() {
Arrays.fill(head, -1);
for (int i = 0; i < (E + 1); i++) {
edge[i] = new Edge(0, 0);
}
addEdge(1, 2);
addEdge(2, 3);
addEdge(2, 5);
addEdge(3, 5);
addEdge(5, 1);
addEdge(5, 4);
}
private void process() {
init();
print();
}
打印的效果:
1
--> 2
2
--> 5
--> 3
3
--> 5
4
5
--> 4
--> 1
数组表示无权值无向图的邻接链表

static class Adj2 {
static Adj2 handler = new Adj2();
public static void main(String[] args) {
handler.process();
}
private void process() {
init();
print();
}
int E = 6;// 边的总数量,当图为无向图时,一条边的两个端点建立邻接表时,均会记录该边,一条边会被记录两次
int V = 5; //顶点的总数量
int idx = 0; //标记当前边的编号
int[] head = new int[(V + 1)]; //每个顶点其中一条边的编号
Edge[] edge = new Edge[(E + 1) << 1]; //边的数量 u-->v v-->u E的数量需要翻倍
public void addEdge(int u, int v) {
edge[++idx].to = v;
edge[idx].next = head[u];
head[u] = idx;
}
class Edge {
int to; // 边所指向的点
int next; //下一条边的编号
public Edge(int to, int next) {
this.to = to;
this.next = next;
}
}
private void init() {
Arrays.fill(head, -1);
for (int i = 0; i < ((E + 1) << 1); i++) {
edge[i] = new Edge(0, 0);
}
int[][] arr = {{1, 2},
{2, 3},
{2, 5},
{3, 5},
{5, 1},
{5, 4}};
for (int i = 0; i < E; i++) {
addEdge(arr[i][0], arr[i][1]);
addEdge(arr[i][1], arr[i][0]);
}
}
private void print() {
for (int i = 1; i <= V; i++) {//遍历所有顶点
System.out.printf("%d\n", i);
for (int j = head[i]; j != -1; j = edge[j].next) {
System.out.printf("--> %d\n", edge[j].to);
}
}
}
}
打印的效果:
1
--> 5
--> 2
2
--> 5
--> 3
--> 1
3
--> 5
--> 2
4
--> 5
5
--> 4
--> 1
--> 3
--> 2
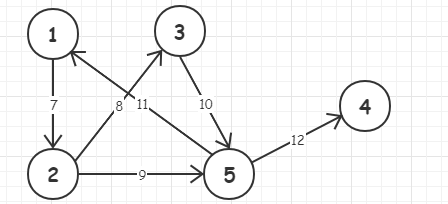
数组表示带权值有向图的邻接链表
static class Adj3 {
static Adj3 handler = new Adj3();
public static void main(String[] args) {
handler.process();
}
private void process() {
init();
print();
}
int E = 6;// 边的总数量,当图为无向图时,一条边的两个端点建立邻接表时,均会记录该边,一条边会被记录两次
int V = 5; //顶点的总数量
int idx = 0; //标记当前边的编号
int[] head = new int[(V + 1)]; //每个顶点其中一条边的编号
Edge[] edge = new Edge[(E + 1)]; //边的数量
public void addEdge(int u, int v, int w) {
edge[++idx].to = v;
edge[idx].w = w;
edge[idx].next = head[u];
head[u] = idx;
}
class Edge {
int to; // 边所指向的点
int next; //下一条边的编号
int w; //边的权值
public Edge(int to, int next, int w) {
this.to = to;
this.w = w;
this.next = next;
}
}
private void init() {
Arrays.fill(head, -1);
for (int i = 0; i < (E + 1); i++) {
edge[i] = new Edge(0, 0, 0);
}
int[][] arr = {{1, 2, 7},
{2, 3, 8},
{2, 5, 9},
{3, 5, 10},
{5, 1, 11},
{5, 4, 12}};
for (int i = 0; i < E; i++) {
addEdge(arr[i][0], arr[i][1], arr[i][2]);
}
}
private void print() {
for (int i = 1; i <= V; i++) {//遍历所有顶点
System.out.printf("u:%d\n", i);
for (int j = head[i]; j != -1; j = edge[j].next) {
System.out.printf("--> v: %d : w: %d\n", edge[j].to, edge[j].w);
}
}
}
}
打印的效果:
u:1
--> v: 2 : w: 7
u:2
--> v: 5 : w: 9
--> v: 3 : w: 8
u:3
--> v: 5 : w: 10
u:4
u:5
--> v: 4 : w: 12
--> v: 1 : w: 11
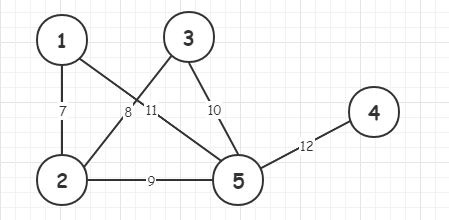
数组表示带权值无向图的邻接链表
static class Adj4 {
static Adj4 handler = new Adj4();
public static void main(String[] args) {
handler.process();
}
private void process() {
init();
print();
}
int E = 6;// 边的总数量,当图为无向图时,一条边的两个端点建立邻接表时,均会记录该边,一条边会被记录两次
int V = 5; //顶点的总数量
int idx = 0; //标记当前边的编号
int[] head = new int[(V + 1)]; //每个顶点其中一条边的编号
Edge[] edge = new Edge[(E + 1) << 1]; //边的数量 u-->v v-->u
public void addEdge(int u, int v, int w) {
edge[++idx].to = v;
edge[idx].w = w;
edge[idx].next = head[u];
head[u] = idx;
}
class Edge {
int to; // 边所指向的点
int next; //下一条边的编号
int w; //边的权值
public Edge(int to, int next, int w) {
this.to = to;
this.w = w;
this.next = next;
}
}
private void init() {
Arrays.fill(head, -1);
for (int i = 0; i < (E + 1) << 1; i++) {
edge[i] = new Edge(0, 0, 0);
}
int[][] arr = {{1, 2, 7},
{2, 3, 8},
{2, 5, 9},
{3, 5, 10},
{5, 1, 11},
{5, 4, 12}};
for (int i = 0; i < E; i++) {
addEdge(arr[i][0], arr[i][1], arr[i][2]);
addEdge(arr[i][1], arr[i][0], arr[i][2]);
}
}
private void print() {
for (int i = 1; i <= V; i++) {//遍历所有顶点
System.out.printf("u:%d\n", i);
for (int j = head[i]; j != -1; j = edge[j].next) {
System.out.printf("--> v: %d : w: %d\n", edge[j].to, edge[j].w);
}
}
}
}
打印的效果:
u:1
--> v: 5 : w: 11
--> v: 2 : w: 7
u:2
--> v: 5 : w: 9
--> v: 3 : w: 8
--> v: 1 : w: 7
u:3
--> v: 5 : w: 10
--> v: 2 : w: 8
u:4
--> v: 5 : w: 12
u:5
--> v: 4 : w: 12
--> v: 1 : w: 11
--> v: 3 : w: 10
--> v: 2 : w: 9
idx索引的问题
其中区别并不大,只是形式1的情况,head的下标就是从1开始,对应的e的下表也是从1开始的,而形式2的情况,他们的下表都是从0开始的。
//形式1
void addEdge(int u, int v, int w)
{
edge[++idx].to = v;
edge[idx].w = w;
edge[idx].next = head[u];
head[u] = idx;
}
//形式2
void addEdge(int u, int v, int w)
{
edge[idx].to = v;
edge[idx].w = w;
edge[idx].next = head[u];
head[u] = idx ++;
}
番外
不要struct来存储
// 建立邻接表存储树
int[] head = new int[N]; // 存储邻接表的表头
int[] edge = new int[N]; // 按输入顺序存储每条边指向的节点
int[] next = new int[N]; // 记录邻接表中当前节点的下一个节点
int idx = 1; // 记录边的序号,边的序号从1开始吧
public void add(int a, int b){
// 第idx边指向b
edge[idx] = b;
// 采用头插法
// 第idx边的下一个节点是上一个时刻的头节点
next[idx] = head[a];
// 当前链表头节点更新,指向第idx边
head[a] = idx;
// idx++ 更新边序号
idx++;
}
尾插法
TODO
Reference
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/10/20/array-mock-adj/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)