状态压缩DP之最短Hamilton路径
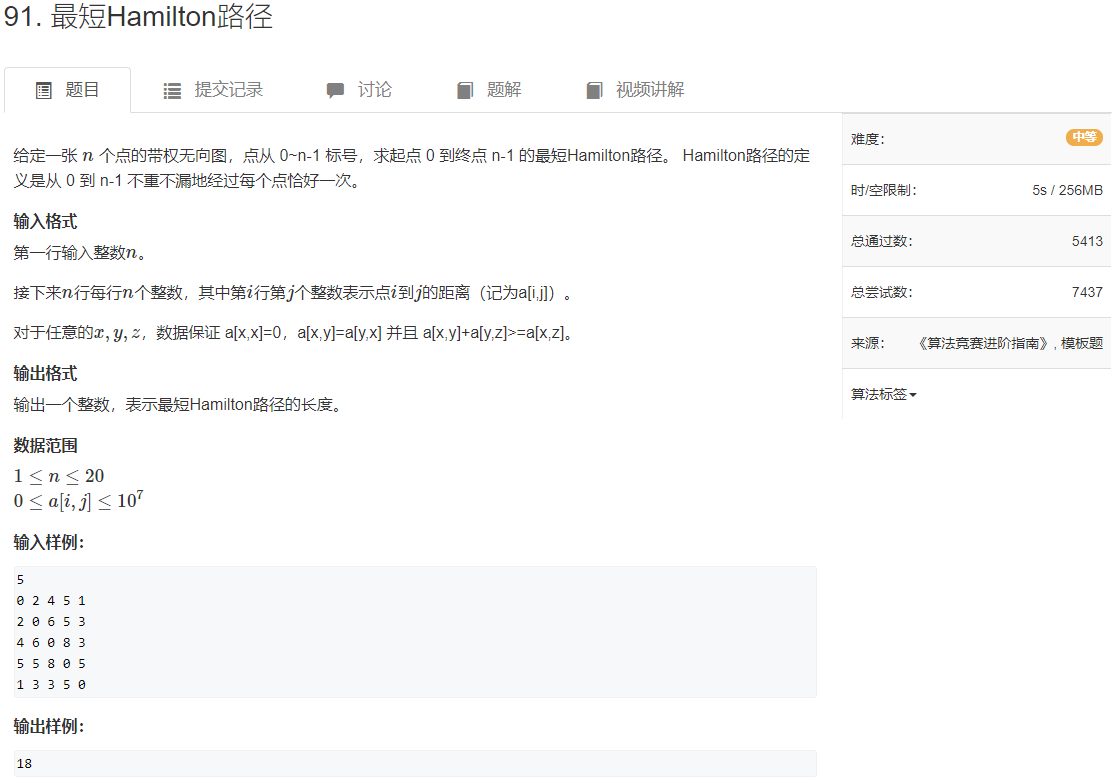
前置知识
模板,见文后链接
int maxn=1<<n; //规定状态的上界
for (int i=0;i<maxn;i++){
if (i&(i<<1)) continue;//如果i情况不成立就忽略
Type[++top]=i;//记录情况i到Type数组中
}
for (int i=1;i<=top;i++){
if (fit(situation[1],Type[i]))
dp[1][Type[i]]=1;//初始化第一层
}
for (int i=2;i<=层数(dp上界);i++){
for (int l=1;l<=top;l++)//穷举本层情况
for (int j=1;j<=top;j++)//穷举上一层情况(上一层对本层有影响时)
if (situation[i],Type[l]和Type[j]符合题意)
dp[i][l]=dp[i][l]+dp[i-1][j];//改变当前层(i)的状态(l)的方案种数
}
for (int i=1;i<=top;i++) ans+=dp[上界][Type[i]];
输入
//手工输入
private static void manualInput() {
Scanner in = new Scanner(System.in);
n = in.nextInt();
G = new int[n][n];
//准备图
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
G[i][j] = in.nextInt();
}
}
}
//自动输入
private static void autoInput() {
n = 5;
G = new int[][]{{0, 2, 4, 5, 1},
{2, 0, 6, 5, 3},
{4, 6, 0, 8, 3},
{5, 5, 8, 0, 5},
{1, 3, 3, 5, 0}};
}
方法1
public static int shortestHamiltonPath() {
//2选1
manualInput();
// autoInput();
dp = new int[1 << n][n];
//初始化dp dp[s][i] 表示走过的集合为s,当前在i点的最小花费
//一共有 1<<n个 状态
for (int s = 0; s < (1 << n); s++) {
for (int i = 0; i < n; i++) {
dp[s][i] = INF >> 1;//在做加法运算时防止溢出int的范围
}
}
dp[1][0] = 0; // 初始化时,顶点0 到 顶点0 的花费为 0
for (int s = 0; s < (1 << n); s++) {
for (int i = 0; i < n; i++) {
if ((s >> i & 1) == 1) {//i 这个点要在集合s中
for (int j = 0; j < n; j++) {//寻找下一个点
/*
走过点的集合s中去除掉点i可以表示为 s - (1 << i),
比方说i是{0,1,4},i是1,那么s = 10011,(1 << i) = 10,s - (1 << i) = 10001
s - (1 << i) >> j 表示找到集合s中j出现的位置
上面的这个 (s - (1 << i) >> j) 与(&)上 1 是为了拿s中的 j位置是否是1 ,是1的话,表示在s集合,不是1的话,也就是0 ,不在s集合中
做这一步是为了要j在集合内,但是已经踢掉了i这个点
i不在 s - (1 << i) 这个集合内, j在 s - (1 << i) 这个集合内
*/
if ((s - (1 << i) >> j & 1) == 1) {
dp[s][i] = Math.min(dp[s][i], dp[s - (1 << i)][j] + G[i][j]);
}
}
}
}
}
//比如说n=5,1<<n 是100000 再-1后 011111 也就是后5位上都为1 要求都走过这5个点
return dp[(1 << n) - 1][n - 1];
}
方法2
public static int shortestHamiltonPath2nd() {
//2选1
// manualInput();
autoInput();
//初始化dp dp[s][i] 表示走过的集合为s,当前在i点的最小花费
dp = new int[1 << n][n];
for (int s = 0; s < (1 << n); s++) {
for (int i = 0; i < n; i++) {
dp[s][i] = INF >> 1;//在做加法运算时防止溢出int的范围
}
}
dp[1][0] = 0; // 初始化时,顶点0 到 顶点0 的花费为 0
for (int s = 0; s < (1 << n); s++) {
for (int now = 0; now < n; now++) {
if ((s >> now & 1) == 0) { //now 不在s集合内 [当前点]
for (int pre = 0; pre < n; pre++) {
if ((s >> pre & 1) == 1) {// pre在s集合内 [下一个点]
int t = s | (1 << now); // 将now这个点加入到s集合中
dp[t][now] = Math.min(dp[t][now], dp[s][pre] + G[pre][now]);
}
}
}
}
}
return dp[(1 << n) - 1][n - 1];
}
入口
import java.util.Scanner;
public class Mian{
static Integer INF = Integer.MAX_VALUE;
static int n; //顶点的个数
static int[][] G; // 图,邻接矩阵表示
static int[][] dp; //dp dp[s][i] 表示走过的集合为s,当前在i点的最小花费 s 是二进制表示状态压缩 state
public static void main(String[] args) {
// shortestHamiltonPath();
shortestHamiltonPath2nd();
}
}
Reference
- https://www.luogu.com.cn/blog/BW-Orzzzzz/dong-tai-gui-hua-wei-yun-suan-yu-zhuang-ya-dp
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/10/14/shortest-hamilton-path/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)