位运算操作常见技巧
基本的位操作
- 与( & )每一位进行比较,两位都为1,结果为1,否则为0(-4 & 1 = 0)
1 0 0 1 1 -->(19)[10] 表示10进制中的19
& 1 1 0 0 1 -->(25)[10]
------------------------------
1 0 0 0 1 -->(17)[10]
- 或 每一位进行比较,两位有一位是1,结果就是1(-4 或 1 = -3)
1 0 0 1 1 -->(19)[10]
| 1 1 0 0 1 -->(25)[10]
------------------------------
1 1 0 1 1 -->(27)[10]
- 非( ~ ) 每一位进行比较,按位取反(符号位也要取反)(~ -4 = 3)
~ 1 0 0 1 1 -->(19)[10]
-----------------------------
0 1 1 0 0 -->(12)[10]
- 异或( ^ )每一位进行比较,相同为0,不同为1(^ -4 = -3)
1 0 0 1 1 -->(19)[10]
^ 1 1 0 0 1 -->(25)[10]
-----------------------------
0 1 0 1 0 -->(10)[10]
- 左移( « ) 整体左移,右边空出位补零,左边位舍弃 (-4 « 1 = -8)
int a = 8;
a << 3;
移位前:0000 0000 0000 0000 0000 0000 0000 1000 -->(8)[10]
移位后:0000 0000 0000 0000 0000 0000 0100 0000 -->(64)[10] 相当于 X 2^3
- 右移( » ) 整体右移,左边空出位补零或补1(负数补1,整数补0),右边位舍弃 (-4 » 1 = -2)
unsigned int a = 8;
a >> 3;
移位前:0000 0000 0000 0000 0000 0000 0000 1000 -->(8)[10]
移位后:0000 0000 0000 0000 0000 0000 0000 0001 -->(1)[10] 相当于 / 2^3
int a = -8;
a >> 3;
移位前:1111 1111 1111 1111 1111 1111 1111 1000 -->(-8)[10]
移位前:1111 1111 1111 1111 1111 1111 1111 1111 -->(-1)[10]
- 无符号右移( »> )同»,但不管正数还是负数都左边位都补0 (-4 »> 1 = 2147483646)
初阶位操作
- 交换两个数
int x = 1 , y = 2;
x^=y; // x = 0011
y^=x; // y = 0001 -->(1)[10]
x^=y; // x = 0010 -->(2)[10]
//x =2, y =1 x变成y y变成x
- 加1操作
int x =1;
x =-(~x); // 0001 --> (~x)后得到1110 --> -(~x) 后得到0010 也就是2,实现了+1操作
//x = 2
- 减1操作
int x =2;
x =~(-x); // 0010 -->(-x)后得到1110 --> ~(-x) 后得到 0001 也就是1,实现了-1操作
- 或 操作和空格转英文字符为小写字符
'a'|' '='a'
// 'a' --> (1100001)[2] 二进制表示 其是(97)[10]
// ' ' --> (0100000)[2] 二进制表示 其是(32)[10]
1100001 -->(97)[10]
| 0100000 -->(32)[10]
------------------------------
1100001 -->(97)[10] 还是'a'本身
'A'|' '='a'
// 'A' --> (1000001)[2] 二进制表示 其是(65)[10]
// ' ' --> (0100000)[2] 二进制表示 其是(32)[10]
1000001 -->(65)[10]
| 0100000 -->(32)[10]
------------------------------
1100001 -->(97)[10] 'A'-->'a'
常用的ASCII值
'0' : 48
'A' : 65
'a' : 97
- 与(&)操作和下划线转英文字符为大写字符
'a'&'_'='A'
// 'a' --> (1100001)[2] 二进制表示 其是(97)[10]
// '_' --> (1011111)[2] 二进制表示 其是(95)[10]
1100001 -->(97)[10]
| 1011111 -->(95)[10]
------------------------------
1000001 -->(65)[10] 'a'-->'A'
'A'&'_'='A'
// 'A' --> (1000001)[2] 二进制表示 其是(65)[10]
// '_' --> (1011111)[2] 二进制表示 其是(95)[10]
1000001 -->(65)[10]
| 1011111 -->(95)[10]
------------------------------
1000001 -->(65)[10] 'A'-->'A'
- 异或(^)操作与空格实现大小写英文字符互转
'a'^' '='A'
// 'a' --> (1100001)[2] 二进制表示 其是(97)[10]
// ' ' --> (0100000)[2] 二进制表示 其是(32)[10]
1100001 -->(97)[10]
^ 0100000 -->(32)[10]
------------------------------
1000001 -->(65)[10] 'a'-->'A'
'A'^' '='a'
// 'A' --> (1000001)[2] 二进制表示 其是(65)[10]
// ' ' --> (0100000)[2] 二进制表示 其是(32)[10]
1000001 -->(65)[10]
^ 0100000 -->(32)[10]
------------------------------
1100001 -->(97)[10] 'A'-->'a'
- 两个数是否异号
int x =-1 , y =2;
x ^ y <0 // true
1111 -->(-1)[10]
^ 0010 -->( 2)[10]
------------------------------
1101 -->(-3)[10] //前面的1111省略掉了
int x =1 , y =2;
x ^ y <0 // false
0001 -->(1)[10]
^ 0010 -->(2)[10]
------------------------------
0011 -->(3)[10]
- 判断奇数偶数:只要根据数的最后一位是 0 还是 1 来决定即可,为 0 就是偶数,为 1 就是奇数
0 == (a & 1) // true的时候是偶数 false时奇数
- 交换符号:将正数变成负数,负数变成正数
整数取反加1,正好变成其对应的负数(补码表示);负数取反加一,则变为其原码,即正数
int reversal(int a) {
return ~a + 1;
}
- 位操作统计二进制中 1 的个数
统计二进制1的个数可以分别获取每个二进制位数,然后再统计其1的个数,此方法效率比较低。这里介绍另外一种高效的方法,同样以 34520 为例,我们计算其 a &= (a-1)的结果:
- 第一次:计算前:1000 0110 1101 1000 计算后:1000 0110 1101 0000
- 第二次:计算前:1000 0110 1101 0000 计算后:1000 0110 1100 0000
- 第三次:计算前:1000 0110 1100 0000 计算后:1000 0110 1000 0000 我们发现,每计算一次二进制中就少了一个 1,则我们可以通过下面方法去统计:
count = 0
while(a){
a = a & (a - 1);
count++;
}
进阶位操作
lowbit:x&(-x)
详解链接,一文掌握数据数组
枚举所有子集
private void enumerateSubset() {
int s, n = 5;
//(1<<n)等价于1*2^n
for (s = 0; s < (1 << n); s++) {
System.out.printf("%s--->", addZeroForNum(Integer.toBinaryString(s), 5));
for (int i = 0; i < n; i++) {
//1<<i 相当于拿2的整数倍数 1 2 4 8 16 这样
if ((s & (1 << i)) != 0) {//不为0时表示true
System.out.printf("%d ", i);
}
}
System.out.printf("\n");
}
}
//比如s = 7 ->二进制数为:00111
//当i = 0,1,2时才输出s=7中的数
//s&(1<<0) == 7&1 == 00111&001 == 1 输出 0
//s&(1<<1) == 7&2 == 00111&010 == 1 输出 1
//s&(1<<2) == 7&4 == 00111&100 == 1 输出 2 分别对应0、1、2下标索引
所有子集:
不选时:\(C_{5}^0\) 1种
选1个元素时:\(C_{5}^1\) 对应:0/1/2/3/4 一共5种
选2个元素时:\(C_{5}^2\) 一共10种
选3个元素时:\(C_{5}^3\) 一共10种
选4个元素时:\(C_{5}^4\) 一共5种
选5个元素时:\(C_{5}^5\) 一共1种
一共32种选择
00000--->
00001--->0
00010--->1
00011--->0 1
00100--->2
00101--->0 2
00110--->1 2
00111--->0 1 2
01000--->3
01001--->0 3
01010--->1 3
01011--->0 1 3
01100--->2 3
01101--->0 2 3
01110--->1 2 3
01111--->0 1 2 3
10000--->4
10001--->0 4
10010--->1 4
10011--->0 1 4
10100--->2 4
10101--->0 2 4
10110--->1 2 4
10111--->0 1 2 4
11000--->3 4
11001--->0 3 4
11010--->1 3 4
11011--->0 1 3 4
11100--->2 3 4
11101--->0 2 3 4
11110--->1 2 3 4
11111--->0 1 2 3 4
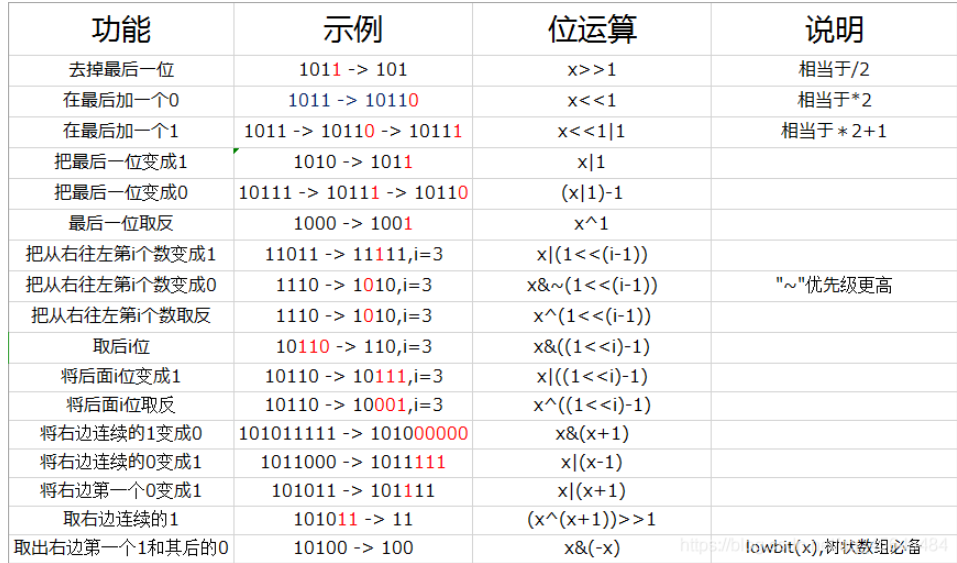
运算符优先级

扩展
转换
/**
* 把2进制字符串key,转成10进制keys
* 数字2代表进制,可以是各种进制,转换成10进制
*
* @param bin
* @return
*/
public static String bin2Ten(String bin) {
String res = String.valueOf(Integer.parseInt(bin, 2));
System.out.printf("binary:%s--->ten:%s\n", bin, res);
return res;
}
private void testOne() {
for (int i = 1; i <= 10; i++) {
int positive = i;
int negative = -i;
String nStr = Integer.toBinaryString(negative);
System.out.println(String.format("%d:%s\t%d:%s\t%s",
positive, addZeroForNum(Integer.toBinaryString(positive), 4)
, negative, nStr.substring(nStr.length() - 4),
addZeroForNum(Integer.toBinaryString(positive & negative), 4)
)
);
}
}
public static String addZeroForNum(String str, int strLength) {
int strLen = str.length();
if (strLen < strLength) {
while (strLen < strLength) {
StringBuffer sb = new StringBuffer();
sb.append("0").append(str);// 左补0
// sb.append(str).append("0");//右补0
str = sb.toString();
strLen = str.length();
}
}
return str;
}
链接
Reference
- https://www.cnblogs.com/td15980891505/p/5447424.html
- https://www.zhihu.com/question/38206659/answer/294900478
- https://www.cnblogs.com/hellocheng/p/7402170.html
- https://www.luogu.com.cn/blog/sxyzsycpqst521/wei-yun-suan-qiang-tai-dei-ling-ren-hai-pa
- http://www.matrix67.com/blog/archives/264(位运算简介及实用技巧)
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/10/14/bit-operate-handbook/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)