ponits ={{0,0},{0,2}};
angle =90;
location={1,1};
  
---
Math.atan2(deltaY, deltaX);
对于{0,0},  Math.atan2(0-1, 0-1)  套入上图的情况3，得到结果是 arctan(y/x)-π=π/4-π=-3*π/4 = -2.356
对于{0,2},  Math.atan2(2-1, 0-1)  套入上图的情况2，得到结果是 arctan(y/x)+π=-π/4+π=3*π/4 =  2.356 
这时候得到的 maxAngle = 90*π/180 = π/2 = 1.571
[-2.356,2.356] , 不能满足这个范围 ，也就是说，2.356 -(-2.356) > 1.571 
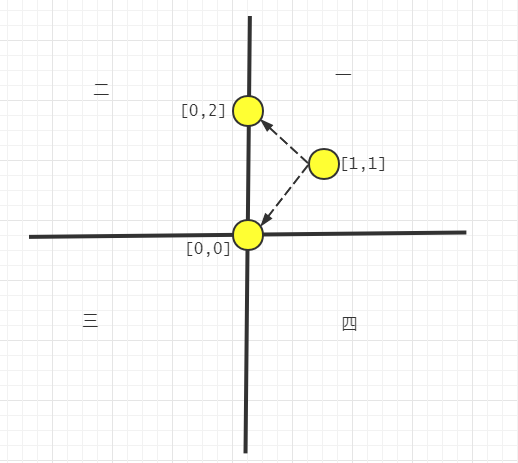
但实际上，从location是可以看到这两个点的，如下图
但是如果每个都加上2π 后，变成这样:
[-2.356,2.356,3.927,8.639]  3.927 是-2.356+ 2π 后的 结果  8.639是2.356+2π 后的 结果
这时候滑动窗口在2.356,3.927时，是可以满足的 3.927(5*π/4) - 2.356(3*π/4) <= 1.571 (π/2)    

    public int visiblePoints(List<List<Integer>> points, int angle, List<Integer> location) {
        List<Double> angles = new ArrayList<>();
        int extraAns = 0;
        for (List<Integer> point : points) {
            int deltaY = point.get(1) - location.get(1);
            int deltaX = point.get(0) - location.get(0);
            if (deltaX == 0 && deltaY == 0) {
                extraAns++;//这种自身的，只需要添加到最后的答案
                continue;
            }
            double tmp = Math.atan2(deltaY, deltaX);
            angles.add(tmp);
           angles.add(tmp + 2 * Math.PI);//如上有解释
        }
        Collections.sort(angles);
        double maxAngle = angle * Math.PI / 180.0; //统一成极坐标
        int r = 0;
        int max = 0;
        for (int l = 0; l < angles.size(); l++) {
            //注意下标越界
            while (r + 1 < angles.size() && angles.get(r + 1) - angles.get(l) <= maxAngle) {
                r++;
            }
            max = Math.max(max, r - l + 1);
        }
        return max + extraAns;
    }