二维矩阵的常见转换技巧
技巧1:二维矩阵按索引拍平到一维数组
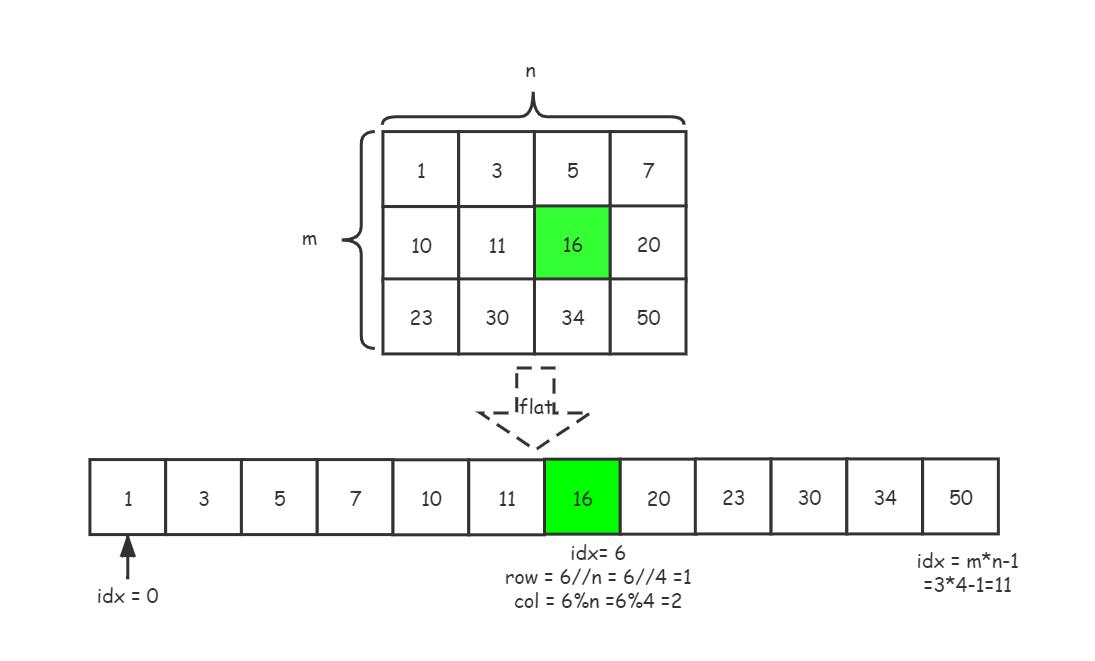
- 如下图所示,每一个二维矩阵对应的,按第1行到第m行依次排列所得到的一维数组的坐标,可以互相转换
如第2行第3列的16这个数,其矩阵的坐标是(1,2),而映射到一维数组的时候,其对应的下标索引idx=6
idx=6=i*n+j=1*4+2=6
而如何通过idx=6反向得到矩阵的坐标呢?
i=idx/n=6/4 =1
j=idx%n=6%4 =2
得到矩阵的坐标为(i,j) ==>(1,2)
技巧2:将矩阵当成二进制转化成十进制
背景知识
对于十进制整数
x,我们可以用x & 1得到x的二进制表示的最低位,它等价于x % 2:例如当
x = 3时,x的二进制表示为11,x & 1的值为1;例如当
x = 6时,x的二进制表示为110,x & 1的值为0。
对于十进制整数
x,我们可以用x & (1 << k)来判断 x 二进制表示的第k位(最低位为第0位)是否为1。如果该表达式的值大于零,那么第k位为1:- 例如当
x = 3时,x的二进制表示为11,x & (1 << 1)=11 & 10=10>0,说明第1位为1; - 例如当
x = 5时,x的二进制表示为101,x & (1 << 1)=101 & 10=0,说明第1位不为1。
- 例如当
举例
给定一个矩阵:
[[0, 0, 1],
[1, 0, 0],
[0, 1, 1]]
该矩阵如果按每行依次排开的话,可以转换成一维矩阵
[0, 0, 1, 1, 0, 0, 0, 1, 1]
将上述的一维矩阵看成一个二进制的数是:
001100011
对应的十进制是99
怎么转化
- 一个矩阵转化成二进制数再转化成十进制数:
/**
*
* @param matrix 二维矩阵
* @param R 矩阵的行数
* @param C 矩阵的列数
* @return
*/
private int encode(int[][] matrix, int R, int C) {
int x = 0;
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
x = x * 2 + matrix[r][c];
}
}
return x;
}
- 一个十进制的数如何转化为二进制的矩阵:
/**
* @param x 源数
* @param R 矩阵的行数
* @param C 矩阵的列数
* @return
*/
private int[][] decode(int x, int R, int C) {
int[][] matrix = new int[R][C];
for (int r = R - 1; r >= 0; r--) {
for (int c = C - 1; c >= 0; c--) {
matrix[r][c] = x & 1;
x >>= 1;
}
}
return matrix;
}
Reference
- https://leetcode-cn.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/solution/zhuan-hua-wei-quan-ling-ju-zhen-de-zui-shao-fan-2/
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/29/two-direction-array-skill/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)