DFS_BFS之打开转盘锁[Saint Bernard]


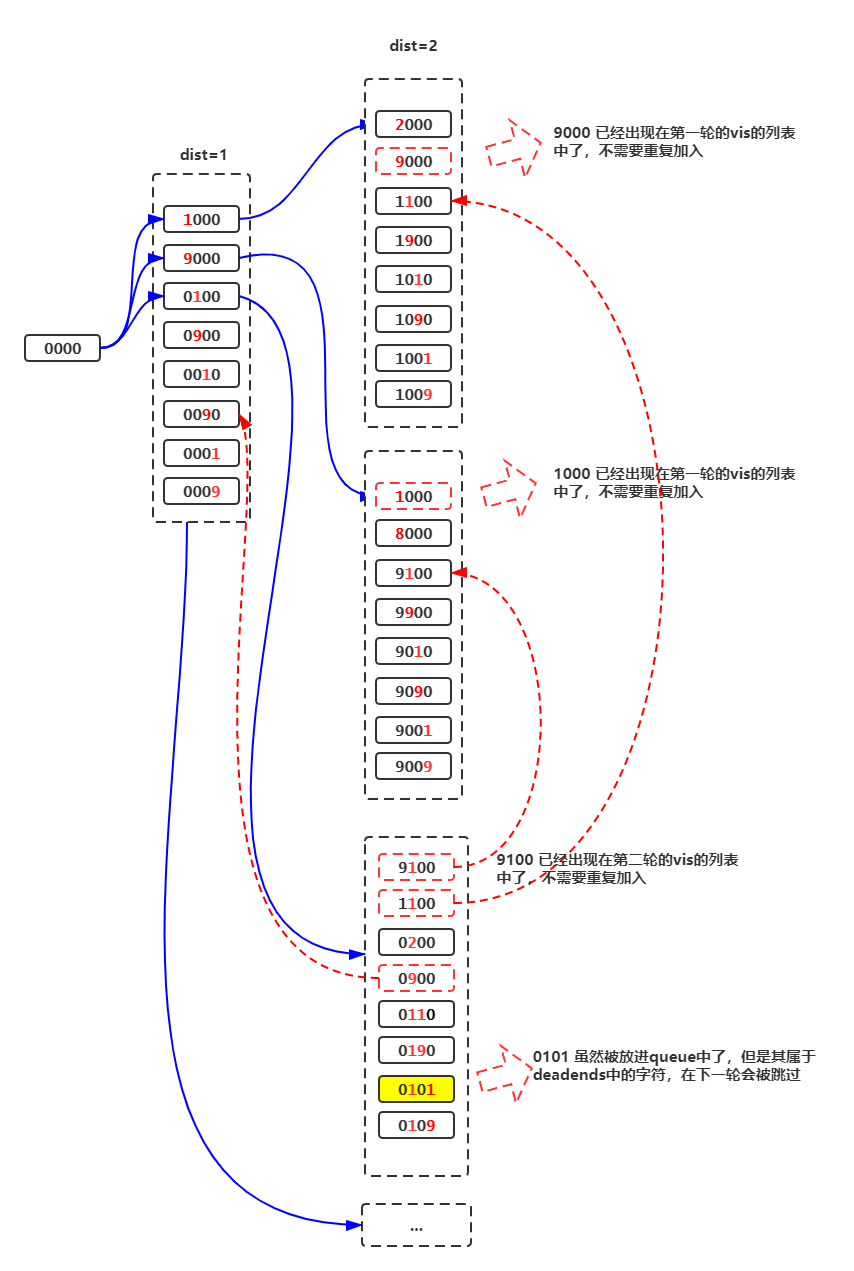
方法1:BFS
public int openLock(String[] deadends, String target) {
//当前处理的转盘字符
Queue<String> queue = new LinkedList<>();
//死亡转盘字符
Set<String> deads = new HashSet<>();
//字符被访问过的列表
Set<String> vis = new HashSet<>();
for (String d : deadends) deads.add(d);
//单个源点触发
queue.offer("0000");
vis.add("0000");
int dist = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String curr = queue.poll();
//跳过死亡转盘字符
if (deads.contains(curr)) continue;
//找到了
if (target.equals(curr)) {
return dist;
}
//四个数每个位置两种选择up down 4*2 =8 种
for (int j = 0; j < 4; j++) {
String up = getUp(curr, j);
//要没被访问过的
if (!vis.contains(up)) {
queue.offer(up);
vis.add(up);
}
String down = getDown(curr, j);
if (!vis.contains(down)) {
queue.offer(down);
vis.add(down);
}
}
}
//层数+1,当前层结束
dist++;
}
return -1;
}
/**
* 生成当前字符往上递增的字符 如 9000-->1000 2000->3000
* @param base
* @param idx
* @return
*/
private String getUp(String base, int idx) {
char[] chas = base.toCharArray();
if (chas[idx] == '9') chas[idx] = '0';
else chas[idx]++;
return String.valueOf(chas);
}
/**
* 生成当前字符往下递增的字符 如 9000-->8000 1000->9000
* @param base
* @param idx
* @return
*/
private String getDown(String base, int idx) {
char[] chas = base.toCharArray();
if (chas[idx] == '0') chas[idx] = '9';
else chas[idx]--;
return String.valueOf(chas);
}
方法2:双向BFS朴素版
常用的ASCII值
'0' : 48
'A' : 65
'a' : 97
public int openLock(String[] deadends, String target) {
Set<String> beginSet = new HashSet<>();
Set<String> endSet = new HashSet<>();
Set<String> deadSet = new HashSet<>(Arrays.asList(deadends));
//使用了额外的visitedSet来装被访问过的str,也可以使用deadSet来访问
Set<String> visitedSet = new HashSet<>();
beginSet.add("0000");
endSet.add(target);
int level = 0;
while (!beginSet.isEmpty() && !endSet.isEmpty()) {
System.out.printf("beginSet:%s\n", JSON.toJSONString(beginSet));
System.out.printf("endSet:%s\n", JSON.toJSONString(endSet));
Set<String> tmpSet = new HashSet<>();
for (String str : beginSet) {
if (endSet.contains(str)) return level;
if (deadSet.contains(str)) continue;
visitedSet.add(str);
for (int i = 0; i < 4; i++) {
char c = str.charAt(i);
String upStr = str.substring(0, i) + ((c == '9' ? '0' : c + 1) - 48) + str.substring(i + 1);
String downStr = str.substring(0, i) + ((c == '0' ? '9' : c - 1) - 48) + str.substring(i + 1);
if (!deadSet.contains(upStr) && !visitedSet.contains(upStr)) {
tmpSet.add(upStr);
}
if (!deadSet.contains(downStr) && !visitedSet.contains(downStr)) {
tmpSet.add(downStr);
}
}
}
level++;
//轮转,上述的for loop中使用的是beginSet,相当于使用beginSet在beginSet与endSet中间来回跳跃
beginSet = endSet;
//本轮的tmpSet值赋值给beginSet
//相当于tmpSet给endSet后备,endSet给beginSet后备
endSet = tmpSet;
}
return -1;
}
方法3:双向BFS优化版
String upStr = str.substring(0, i) + (c == '9' ? 0 : c - '0' + 1) + str.substring(i + 1);
String downStr = str.substring(0, i) + (c == '0' ? 9 : c - '0' - 1) + str.substring(i + 1);
//注意? 后面的 0 与'0'
public int openLock(String[] deadends, String target) {
Set<String> beginSet = new HashSet<>();
Set<String> endSet = new HashSet<>();
Set<String> deadSet = new HashSet<>(Arrays.asList(deadends));
beginSet.add("0000");
endSet.add(target);
int level = 0;
while (!beginSet.isEmpty() && !endSet.isEmpty()) {
//选取小的set来进行,swap操作
if (beginSet.size() > endSet.size()) {
Set<String> tmpSet = beginSet;
beginSet = endSet;
endSet = tmpSet;
}
Set<String> tmpSet = new HashSet<>();
for (String str : beginSet) {
if (endSet.contains(str)) return level;
if (deadSet.contains(str)) continue;
deadSet.add(str);
for (int i = 0; i < 4; ++i) {
char c = str.charAt(i);
String upStr = str.substring(0, i) + (c == '9' ? 0 : c - '0' + 1) + str.substring(i + 1);
String downStr = str.substring(0, i) + (c == '0' ? 9 : c - '0' - 1) + str.substring(i + 1);
System.out.printf("upStr:%s,downStr:%s\n", upStr, downStr);
if (!deadSet.contains(upStr)) {
tmpSet.add(upStr);
}
if (!deadSet.contains(downStr)) {
tmpSet.add(downStr);
}
}
}
level++;
//这一轮的beginSet已经用完了,用tmpSet来覆盖
beginSet = tmpSet;
}
return -1;
}
Reference
- https://leetcode.com/problems/open-the-lock/discuss/110237/Regular-java-BFS-solution-and-2-end-BFS-solution-with-improvement
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/27/open-the-lock/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)