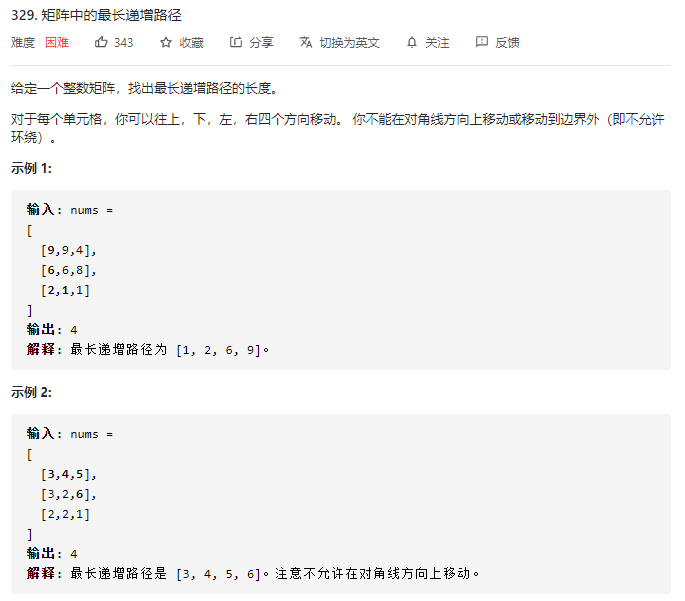
DFS_BFS之 矩阵中的最长递增路径[Collie]

方法1:记忆化搜索
思路
memo[i][j]表示的是以(i,j)为起点出发,沿着其上下左右四个方向,能形成的最长的递增路径的长度- 为什么只需要判断其周边的四个方向即可呢?如果
(i,j)点的值要小于周边的点,那么(i,j)这个点可以接到其周边的点上去,然后在总长度上+1
下面例子
//元素的matrix
9, 9, 4
6, 6, 8
2, 1, 1
//打印的memo,见代码的注释行
1 0 0
0 0 0
0 0 0
--------------
1 1 0
0 0 0
0 0 0
--------------
1 1 2
0 0 1
0 0 0
--------------
1 1 2
2 0 1
0 0 0
--------------
1 1 2
2 2 1
0 0 0
--------------
1 1 2
2 2 1
0 0 0
--------------
1 1 2
2 2 1
3 0 0
--------------
1 1 2
2 2 1
3 4 0
--------------
1 1 2
2 2 1
3 4 2
--------------
int[][] memo;
int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
int m, n;
public int longestIncreasingPath(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
m = matrix.length;
n = matrix[0].length;
memo = new int[m][n];
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
res = Math.max(res, dfs(matrix, i, j));
// PrintUtils.printMatrix(memo);
}
}
return res;
}
private int dfs(int[][] matrix, int i, int j) {
if (memo[i][j] != 0) return memo[i][j];
memo[i][j] += 1;
for (int[] dir : directions) {
int nextI = i + dir[0], nextJ = j + dir[1];
if (inArea(nextI, nextJ) && matrix[i][j] < matrix[nextI][nextJ]) {
memo[i][j] = Math.max(memo[i][j], dfs(matrix, nextI, nextJ) + 1);
}
}
return memo[i][j];
}
private boolean inArea(int i, int j) {
return i >= 0 && i < m && j >= 0 && j < n;
}
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/26/longest-increasing-path-in-a-matrix/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)