一文掌握Prim算法
思路
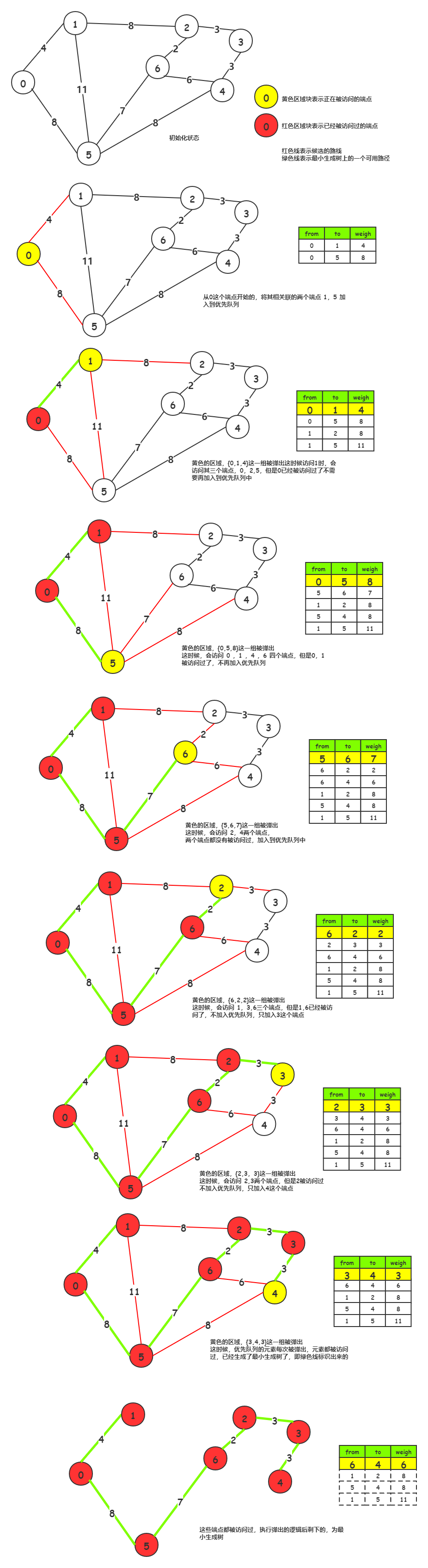
Prim 算法是依据顶点来生成的,它的每一步都会为一颗生长中的树添加一条边,一开始这棵树只有一个顶点,然后会添加 N - 1 条边,每次都是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中。 算法流程:
- 记录每个顶点到其他顶点的权重;
- 设计一个
boolean[],判断是否被读取过; - 每次读取堆顶元素,如果曾经被读取过就不再读取,否则把其所有边加入堆;
static class Pair {
int start;//from
int end;//to
int weigh;//weigh
public Pair(int start, int end, int weigh) {
this.start = start;
this.end = end;
this.weigh = weigh;
}
}
static int V = 7;//顶点或者端点的个数
public static void testOne() {
int E = 10;//端点之间形成的边的个数
int[][] edges = {{0, 1, 4},//边的详细信息 from to weigh
{0, 5, 8},
{1, 2, 8},
{1, 5, 11},
{2, 3, 3},
{2, 6, 2},
{3, 4, 3},
{4, 5, 8},
{4, 6, 6},
{5, 6, 7},
};
//构造graph
Map<Integer, List<Pair>> graph = new HashMap<>();
for (int i = 0; i < E; i++) {
int start = edges[i][0];
int end = edges[i][1];
int weigh = edges[i][2];
graph.putIfAbsent(start, new ArrayList<>());
graph.putIfAbsent(end, new ArrayList<>());
graph.get(start).add(new Pair(start, end, weigh));
graph.get(end).add(new Pair(end, start, weigh));
}
int minCost = prim(0, graph);
System.out.println(minCost);
for (Pair pair : mst) {
System.out.println(String.format("from:%d,to:%d,weigh:%d", pair.start,
pair.end, pair.weigh));
}
}
//最小生成树
public static List<Pair> mst = new ArrayList<>();
public static int prim(int start, Map<Integer, List<Pair>> graph) {
//记录每个端点是否被访问过
boolean[] visited = new boolean[V];
//按权值从小到大的堆
PriorityQueue<Pair> minHeap = new PriorityQueue<>((o1, o2) -> o1.weigh - o2.weigh);
//开始的点,触发堆的轮转
minHeap.offer(new Pair(-1, start, 0));
//最小路径和
int minCost = 0;
while (!minHeap.isEmpty()) {
//弹出堆顶的最小权值在Pair
Pair curr = minHeap.poll();
//拿到其端点
start = curr.end;
//端点被访问过,返回
if (visited[start]) continue;
if (curr.start != -1) mst.add(curr);//生成mst
//标记
visited[start] = true;
//更新权值
minCost += curr.weigh;
//遍历端点的候选端点,如果候选端点被访问过,不需要加入到堆中
List<Pair> candidates = graph.get(start);
for (int i = 0; i < candidates.size(); ++i) {
if (!visited[candidates.get(i).end]) {
minHeap.offer(candidates.get(i));
}
}
}
return minCost;
}
output
27
from:0,to:1,weigh:4
from:0,to:5,weigh:8
from:5,to:6,weigh:7
from:6,to:2,weigh:2
from:2,to:3,weigh:3
from:3,to:4,weigh:3
举例:1135.最低成本联通所有城市

/**
* @param N 顶点的数量
* @param connections 顶点与边之间的信息
* @return
*/
public int minimumCost(int N, int[][] connections) {
if (N <= 1 || connections == null || connections.length < N - 1) return -1;
Map<Integer, ArrayList<int[]>> graph = new HashMap<>();
//构造图
for (int[] connect : connections) {
int start = connect[0];
int end = connect[1];
int weigh = connect[2];
graph.putIfAbsent(start, new ArrayList<>());
graph.get(start).add(new int[]{end, weigh});
graph.putIfAbsent(end, new ArrayList<>());
graph.get(end).add(new int[]{start, weigh});
}
//选取第一个为端点
boolean[] visited = new boolean[N];
int start = connections[0][0];
//下标索引从0开始,需要-1
visited[start - 1] = true;
PriorityQueue<int[]> pq = new PriorityQueue<>(((o1, o2) -> o1[1] - o2[1]));
pq.addAll(graph.get(start));
int minCost = 1;
int count = 1;
while (!pq.isEmpty()) {
int[] curr = pq.poll();
//该顶点被访问过,跳过,找下一个顶点
if (visited[curr[0] - 1]) continue;
pq.addAll(graph.get(curr[0]));
//更新最小生成树权值,以及访问顶点数量
minCost += curr[1];
count++;
//当端点被访问结束,即可退出
if (count == N) return minCost;
}
return -1;
}
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/23/prim-algorithm-master/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)