一文掌握Dijkstra算法
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
基本思想
- 通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
- 此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
- 初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是”起点s到该顶点的路径”。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 … 重复该操作,直到遍历完所有顶点。
操作步骤
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
- 从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
- 重复步骤(2)和(3),直到遍历完所有顶点。
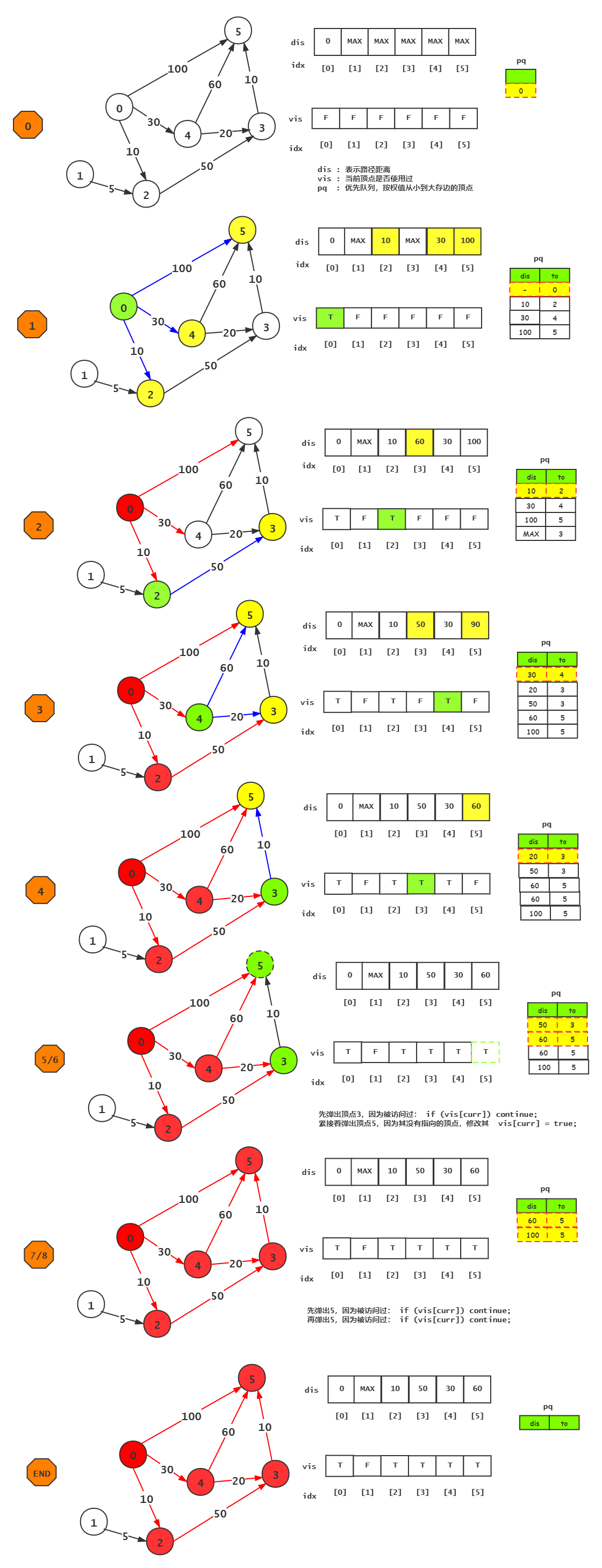
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
核心代码
/**
* @param edges 传入的边
* @param s 起始顶点
* @param n
* @return
*/
public int[] dijkstra(int[][] edges, int s, int n) {
Map<Integer, List<int[]>> graph = new HashMap<>();
for (int[] edge : edges)
graph.computeIfAbsent(edge[0], e -> new ArrayList<>()).add(new int[]{edge[1], edge[2]});
int[] dis = new int[n];
Arrays.fill(dis, Integer.MAX_VALUE);
boolean[] vis = new boolean[n];
dis[s] = 0;
PriorityQueue<Integer> pq = new PriorityQueue<>(((o1, o2) -> dis[o1] - dis[o2]));
pq.offer(s);
while (!pq.isEmpty()) {
int curr = pq.poll();
if (vis[curr]) continue;
vis[curr] = true;
List<int[]> nexts = graph.getOrDefault(curr, new ArrayList<>());
for (int[] next : nexts) {
int to = next[0];
int weigh = next[1];
if (vis[to]) continue;
if (dis[to] > dis[curr] + weigh) {
dis[to] = dis[curr] + weigh;
}
pq.offer(to);
}
}
return dis;
}
测试
private void testOne() {
int n = 6;//顶点数量
int s = 0;//起点的下标索引
int e = 8;//边的数量
int[][] edges = new int[e][3];
edges[0] = new int[]{0, 2, 10};
edges[1] = new int[]{0, 4, 30};
edges[2] = new int[]{0, 5, 100};
edges[3] = new int[]{1, 2, 5};
edges[4] = new int[]{2, 3, 50};
edges[5] = new int[]{3, 5, 10};
edges[6] = new int[]{4, 3, 20};
edges[7] = new int[]{4, 5, 60};
// System.out.println(JSON.toJSONString(edges));
dijkstra(edges, s, n);
}
Reference
- https://blog.csdn.net/heroacool/article/details/51014824
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/23/dijkstra-algorithm-master/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)