一文掌握Bellman-Ford算法
方法1:朴素版
Bellman-Ford算法思想
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
Bellman-Ford算法流程分为三个阶段:
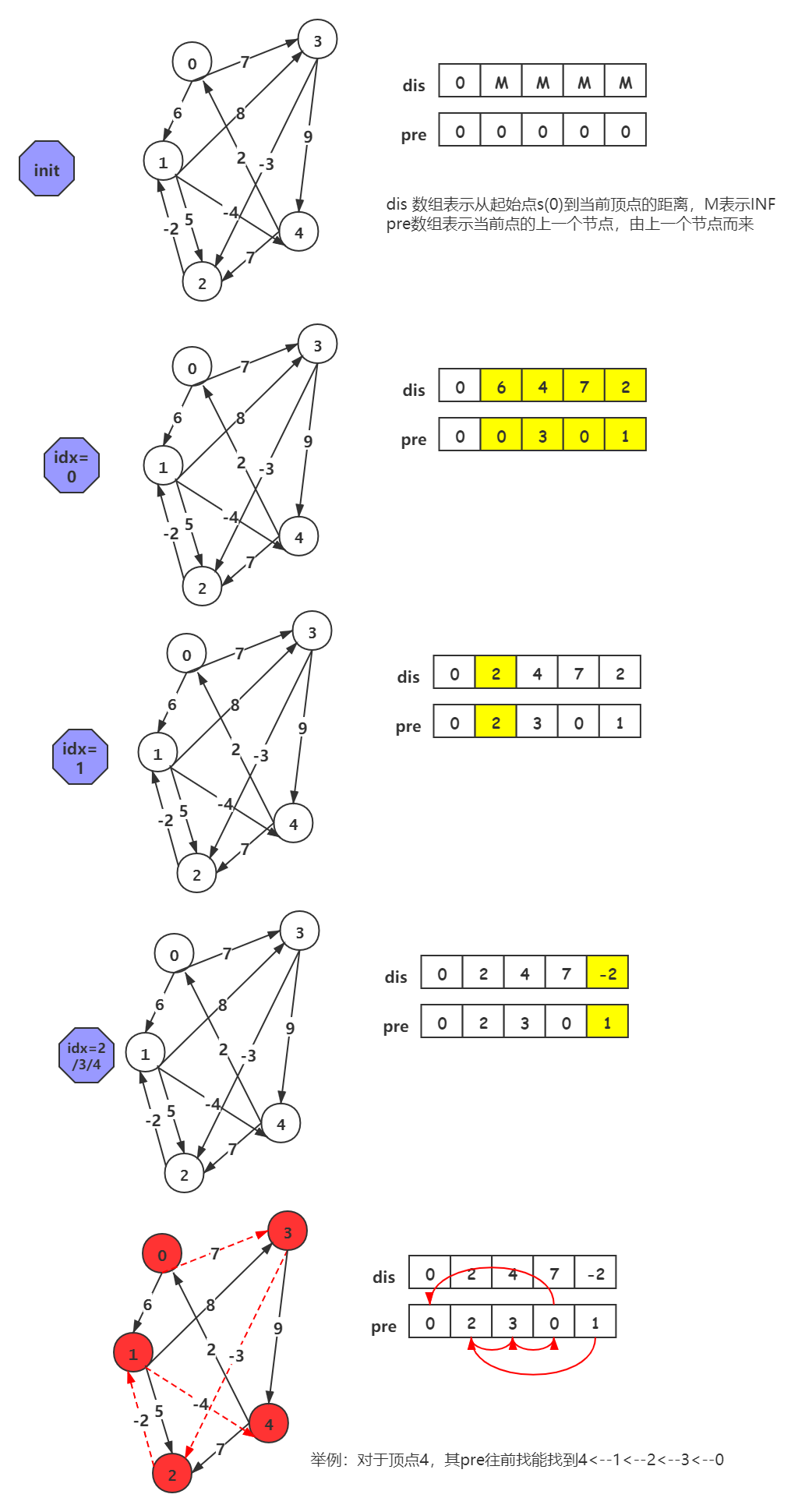
(1) 初始化:将除源点外的所有顶点的最短距离估计值 d[v] ←+∞, d[s] ←0;
(2) 迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行 v -1次) (3) 检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
G:图G
E(G):边的集合
S: 源顶点
Dis[i]:表示s到i的最短距离,初始为+∞
D[s]=0;
for (int i=0;i<|v|-1;i++)
for each (u,v)∈E(G)
if(dis[u]+w(u,v)<dis[v]
dis[v]=dis[u]+w(u,v);
for each (u,v)∈E(G)
if(d[v]>d[u]+w(u,v)
return false;//返回false,说明存在负权回路
return true;
Bellman - ford算法是求含负权图的单源最短路径的一种算法,效率较低(O(nm)),代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成.
为什么是松弛n-1次?简单来说就是从源点到一个点的最短路最极限的一种情况的路径需要经过全部的点,也就是需要松弛v-1次,这样,我们执行v-1次就可以保证所有的点都松弛到最佳的情况,如果执行了v-1次后还能继续松弛,那就说明图中有负权环,无解.
bellman的松弛操作有点类似于Dijkstra算法,是对u->v以及u->k->v(k为中间值)取最小值,n-1次松弛后,dis数组中储存的即为要求点到各个点之间的最小值.
int dis[maxn];
struct edge{
int u,v; ///起点,终点
int w; ///权值
}e[maxn];
int n,m; //n为点,m为边的总数
bool bellman(int s,int n) ///求a->其他点的最短路,n为结点总数.可判负环
{
memset(dis,inf,(n+1)<<2); //将数组前n+1个数初始化为INF
dis[s]=0;
For(i,n-1) ///for(int i=0;i<n-1;i++),下同
For(j,m)
dis[e[j].v]=min(dis[e[j].v],dis[e[j].u]+e[j].w); ///松弛操作,即上文的u->v和u->k->v
For(i,m) ///松弛完后还能再松弛即代表有负环
if(dis[e[i].v]>dis[e[i].u]+e[i].w)
return true;
return false;
}
实现
Bellman-Ford算法可以大致分为三个部分 第一,初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。 第二,进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。 第三,遍历途中所有的边(edge(u,v)),判断是否存在这样情况: d(v) > d (u) + w(u,v) 则返回false,表示途中存在从源点可达的权为负的回路。
主体代码
int n;//顶点个数
int e;//边的数量
Integer INF = Integer.MAX_VALUE;
int[] dis;//存储当前顶点的路径
int[] pre;//存储上来自的顶点
/**
* @param s 起点
* @return
*/
public boolean bellmanFord(int s, Edge[] edges) {
//初始化
for (int i = 0; i < n; i++) {
dis[i] = i == s ? 0 : INF;
}
//每一轮的顶点,对所有的edges做松弛
for (int i = 0; i < n; i++) {
for (int j = 0; j < e; j++) {
if (dis[edges[j].v] > dis[edges[j].u] + edges[j].w) {//relax操作
dis[edges[j].v] = dis[edges[j].u] + edges[j].w;
pre[edges[j].v] = edges[j].u;
}
}
}
//
boolean f = false;
for (int i = 0; i < e; i++) {
if (dis[edges[i].v] > dis[edges[i].u] + edges[i].w) {
f = true;
break;
}
}
// printPath();
return f;
}
结构
public class Edge {
public int u;//from
public int v;//to
public int w;//weigh
public Edge(int u, int v, int w) {
this.u = u;
this.v = v;
this.w = w;
}
}
测试
public void testOne() {
n = 5;
e = 9;
Edge[] edges = new Edge[e];
edges[0] = new Edge(0, 1, 6);
edges[1] = new Edge(0, 3, 7);
edges[2] = new Edge(1, 2, 5);
edges[3] = new Edge(1, 3, 8);
edges[4] = new Edge(1, 4, -4);
edges[5] = new Edge(2, 1, -2);
edges[6] = new Edge(3, 2, -3);
edges[7] = new Edge(3, 4, 9);
edges[8] = new Edge(4, 0, 2);
int s = 0;
dis = new int[n];
pre = new int[n];
bellmanFord(s, edges);
}
辅助
打印路径
public void printPath() {
for (int i = 0; i < n; i++) {
System.out.printf("v:%d,dis:%d,", i, dis[i]);
getPath(i);
}
}
public void getPath(int root) {
while (root != pre[root]) {
System.out.printf("%d<--", root);
root = pre[root];
}
if (root == pre[root]) {
System.out.printf("%d\n", root);
}
}
打印的结果
v:0,dis:0,0
v:1,dis:2,1<--2<--3<--0
v:2,dis:4,2<--3<--0
v:3,dis:7,3<--0
v:4,dis:-2,4<--1<--2<--3<--0
Reference
- https://blog.csdn.net/bestsort/article/details/80100039
- http://www.cppblog.com/kuramawzw/archive/2009/08/12/93085.html
- https://blog.csdn.net/qq_40984919/article/details/80489441
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/22/bellman-ford-algorithm-master/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)