动态规划解整除数组[Swan]

官方题解
在阐述解决方案之前,我们给出一些可以从模运算的性质中得到的推论,这些推论将在后面中用到。
给定升序序列(即 E < F < G)[E, F, G],并且该列表本身满足问题中描述的整除子集,就不必枚举该子集的所有数字,在以下两种情况:
推论一:可除以整除子集中的最大元素的任何值,加入到子集中,可以形成另一个整除子集,即对于所有 h,若有 h % G == 0,则 [E, F, G, h] 形成新的可除子集。 推论二:可除以整除子集中最小元素的任何值,加入到子集中,可以形成另一个整除子集,即,对于所有的 d,若有 E % d == 0,则 [d, E, F, G] 形成一个新的整除子集。 上面两个推论可以帮助我们构造一个有效的解决方案。
方法1:DP
public List<Integer> largestDivisibleSubset(int[] nums) {
if (nums == null || nums.length == 0) return new ArrayList<>();
//排序
Arrays.sort(nums);
int n = nums.length;
List<ArrayList> resList = new ArrayList<>();
for (int num : nums) resList.add(new ArrayList());
List<Integer> ans = new ArrayList();
for (int i = 0; i < n; ++i) {
//当前处理的以nums[i]结尾的集合
List currList = resList.get(i);
List<Integer> levelList = new ArrayList<>();
for (int k = 0; k < i; ++k) {
//求最大且要判断当前元素是否与nums[k]是否整除
if (nums[i] % nums[k] == 0 && levelList.size() < resList.get(k).size()) {
levelList = resList.get(k);
}
}
currList.addAll(levelList);
currList.add(nums[i]);
//记录下最大的
if (currList.size() > ans.size()) ans = currList;
}
return ans;
}
复杂度分析:
- 时间复杂度:
O(N^2) - 空间复杂度:
O(N^2)
方法2:DP-Space(O(1))
public List<Integer> largestDivisibleSubset(int[] nums) {
if (nums == null || nums.length == 0) return new ArrayList<>();
//排序
Arrays.sort(nums);
int n = nums.length;
//dp[i]表示以当前元素nums[i]结尾形成的整除子集的最长长度
int[] dp = new int[n];
//最大的子集长度大小,最大的子集的以nums[i]结尾的数字的索引i
int maxSubsetSize = -1, maxSubsetIdx = -1;
for (int i = 0; i < n; ++i) {
//当前这一个i下的这一轮的子集大小
int subsetSize = 0;
for (int k = 0; k < i; ++k) {
//可以整除+当前的大小小于以nums[k]结束的子集的大小,可以将nums[i]追加到子集中
if (nums[i] % nums[k] == 0 && subsetSize < dp[k]) {
subsetSize = dp[k];
}
}
//更新当前子集的大小,以nums[i]结尾的子集
//更新最大的子集长度大小,最大的子集的以nums[i]结尾的数字的索引i
dp[i] = subsetSize + 1;
if (maxSubsetSize < dp[i]) {
maxSubsetSize = dp[i];
maxSubsetIdx = i;
}
}
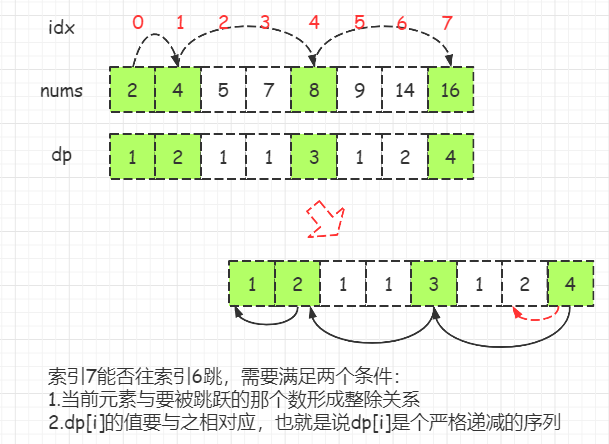
//开始往回找,因为已经记录下最大的子集的最末尾的数nums[maxSubsetIdx]
int currNum = nums[maxSubsetIdx], currSize = maxSubsetSize;
LinkedList<Integer> ans = new LinkedList<>();
for (int i = maxSubsetIdx; i >= 0; i--) {
if (currSize == 0) break;
//需要满足的两个条件,见图
if (currNum % nums[i] == 0 && currSize == dp[i]) {
ans.addFirst(nums[i]);
currNum = nums[i];
currSize--;
}
}
return ans;
}
方法3:递归
TODO
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/09/13/largest-divisible-subset/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)