图问题之地图分析[Apis Cerana]


0.2.BFS模板
def bfs(){
q.push(head);//一般为q这种优先队列来处理bfs问题
level;//记录层数
while(!q.empty()){
size = q.size;
for i in range(size):
temp=q.front;//弹出元素
q.pop();
if(temp为目标状态)输出解
if(temp不合法)continue;
if(temp合法)q.push(temp+Δ);
level++;//for loop 结束后层数扩张一层
}
}
一般也会设置一些visit[] 来记录元素访问与否,做剪枝
这一题类似01矩阵
方法1:BFS(记录层数)
- 需要做一次额外判断,当
grid全是陆地或者全是海洋时,返回-1 bfs的循环要找到海洋的点的坐标- 初始化时有多个出发源点,本题是为陆地的坐标点
如下图的case
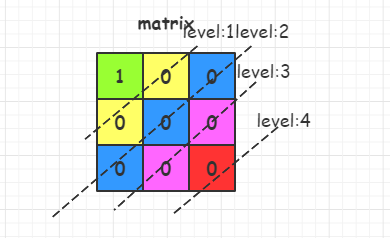
- 初始化的
queue装入的是陆地(也就是值为1)的坐标,
public int maxDistance(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) queue.add(new int[]{i, j});
}
}
//全为0或者全为1的时候返回-1
if (queue.isEmpty() || queue.size() == m * n) return -1;
int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};//对应了上右下左四个方向
int level = -1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int k = 0; k < size; k++) {
int[] curr = queue.poll();
int currX = curr[0], currY = curr[1];
for (int[] d : dirs) {
int nextX = currX + d[0], nextY = currY + d[1];
if (nextX < 0 || nextX >= m || nextY < 0 || nextY >= n || grid[nextX][nextY] == 1) continue;
queue.offer(new int[]{nextX, nextY});
grid[nextX][nextY] = 1;
}
}
level++;
}
return level;
}
方法2:BFS(不记录层数)
- 记录最大值,原地修改
grid
public int maxDistance(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) queue.add(new int[]{i, j});
}
}
//全为0或者全为1的时候返回-1
if (queue.isEmpty() || queue.size() == m * n) return -1;
int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};//对应了上右下左四个方向
int res = -1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int k = 0; k < size; k++) {
int[] curr = queue.poll();
int currX = curr[0], currY = curr[1];
for (int[] d : dirs) {
int nextX = currX + d[0], nextY = currY + d[1];
if (nextX < 0 || nextX >= m || nextY < 0 || nextY >= n || grid[nextX][nextY] != 0) continue;
queue.offer(new int[]{nextX, nextY});
grid[nextX][nextY] = grid[currX][currY] + 1;
res = Math.max(res, grid[nextX][nextY] - 1);
}
}
}
return res;
}
文档信息
- 本文作者:wat1r
- 本文链接:https://wat1r.github.io/2020/08/27/as-far-from-land-as-possible/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)